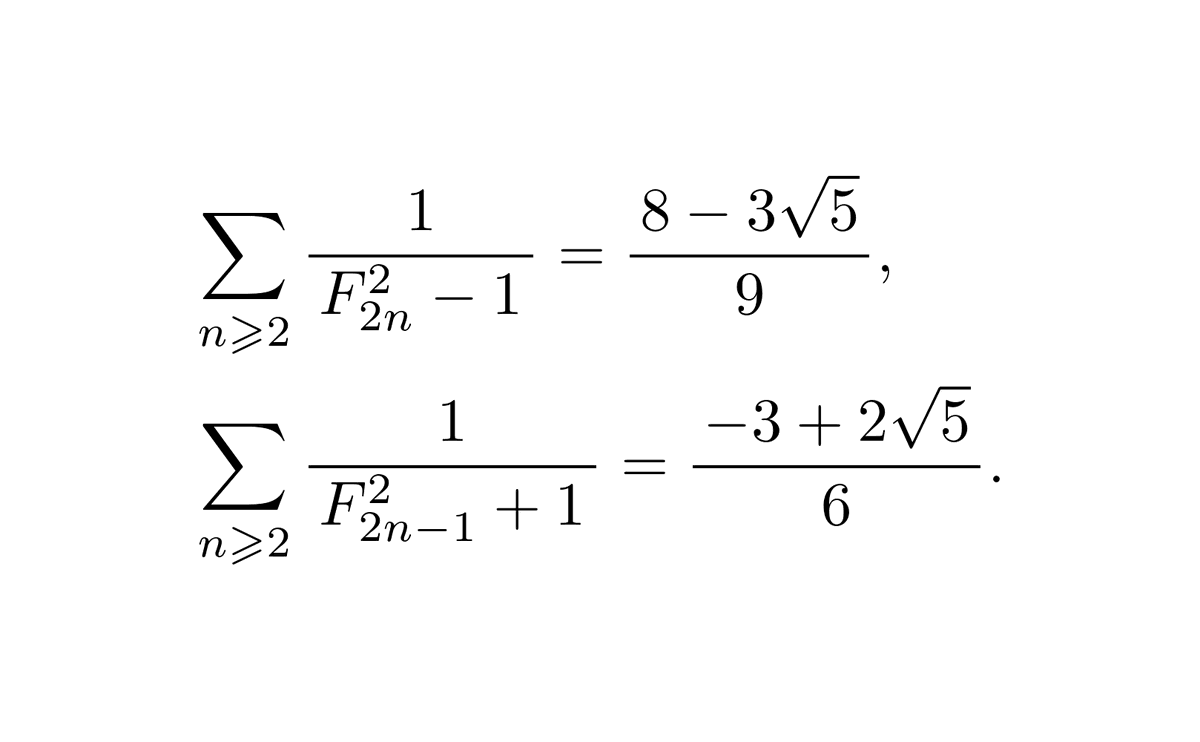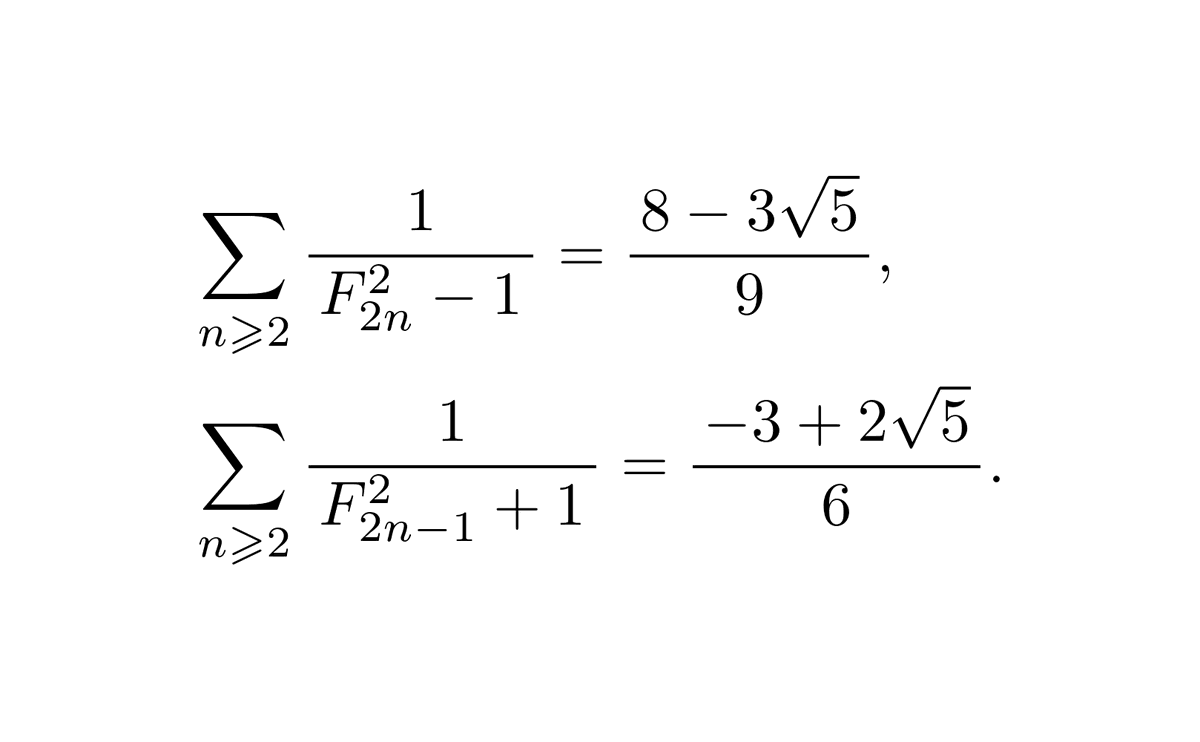フィボナッチ数列の逆数和

数学において、フィボナッチ数列の逆数和（フィボナッチすうれつのぎゃくすうわ、英: reciprocal Fibonacci constant）、またはψは、フィボナッチ数列の逆数の総和として定義される数学定数である。

${\displaystyle \psi =\sum _{k=1}^{\infty }{\frac {1}{F_{k}}}={\frac {1}{1}} {\frac {1}{1}} {\frac {1}{2}} {\frac {1}{3}} {\frac {1}{5}} {\frac {1}{8}} {\frac {1}{13}} {\frac {1}{21}} \cdots .}$

この和の連続した項の比は、黄金比の逆数に近づく。従って、ダランベールの収束判定法により、この和は収束する。

ψの値は、おおよそで以下のようになると知られている。

${\displaystyle \psi =3.359885666243177553172011302918927179688905133731\dots .}$

ビル・ゴスパーは、この値の高速な数値近似のためのアルゴリズムを得た。フィボナッチ数列の逆数和自身はk個の項に対しO(k)桁の精度であるが、ゴスパーのSeries accelerationではk個の項に対しO(k ²)桁の精度である。

ψは無理数であると知られている。これはポール・エルデシュ、ロナルド・グラハム、Leonard Carlitzなどにより予想され、1989年、Richard André-Jeanninによって証明された。 フィボナッチ数列の逆数和が超越数(代数的数でない数)であるかは、分かっていない。

連分数展開(数列表記)は、

${\displaystyle \psi =[3;2,1,3,1,1,13,2,3,3,2,1,1,6,3,2,4,362,2,4,8,6,30,50,1,6,3,3,2,7,2,3,1,3,2,\dots ]\!\,}$

のようになる。

脚注

関連項目

• フィボナッチ数列
• 逆数の和の一覧

外部リンク

• Weisstein, Eric W. "Reciprocal Fibonacci Constant". mathworld.wolfram.com (英語).