ナビエ–ストークス方程式

ナビエ–ストークス方程式（ナビエ–ストークスほうていしき、英: Navier–Stokes equations）は、流体の運動を記述する2階非線型偏微分方程式であり、流体力学で用いられる。アンリ・ナビエとジョージ・ガブリエル・ストークスによって導かれた。日本語の文献だと「NS方程式」とも略される。ナビエ・ストークス方程式は、ニュートン力学における運動の第2法則に相当する。

導出

流体の質量保存の法則と運動量保存の法則を表す連続の方程式

を用いると、流れの速度場 ${\boldsymbol {v}}$ の物質微分は

と導かれる。ここで、 $\rho$ は密度場、 ${\boldsymbol {\sigma }}$ は応力場、 ${\boldsymbol {g}}$ は流体の単位質量あたりに作用する外力場（加速度場）である。

ここで、ニュートン流体を仮定すれば、応力場が

で与えられる。ただし、 $p$ は圧力（静圧）、 $\chi$ は体積粘性率、 $\mu$ は剪断粘性率である。 ${\boldsymbol {e}}$ は対称化した速度勾配で、デカルト座標の下で成分表示をすれば

で表され、 $\Theta$ は速度場の発散

である。

この形の応力場 ${\boldsymbol {\sigma }}$ を用いると、速度場 ${\boldsymbol {v}}$ の物質微分が

で与えられる。この方程式がナビエ–ストークス方程式である。この3本の連立偏微分方程式を解いて3次元ベクトル ${\boldsymbol {v}}$ とスカラー $p$ の計4つの未知関数の一般解が常に存在する（もしくは一般解が存在しないケースがある）ことを証明せよ、という問題が「ナビエ–ストークス方程式の解の存在と滑らかさ（ミレニアム懸賞問題の1つ）」である。加えて、それらの解が「時間大域的かつ滑らかな解」なのかどうかも、非常に重要な論点となる。

なお、速度場の物質微分の第二項は「対流項」あるいは「移流項」と呼ばれ、ベクトル解析の公式により、

と変形することができる。ここで ω は速度場の回転

であり、渦度と呼ばれる。

単純化した方程式

ナビエ–ストークス方程式は非線形であり、複雑過ぎるので解を求めることは困難である。このため、いくつかの仮定をして問題を簡単化することが多い。しかし簡単化された方程式ですら解析的な方法では解が得られないことが普通であり、解の存在性などの定性的な議論を超えて、具体的な解の様子を知るためには、ほとんどの場合に数値的な近似解法が必要になる。

非圧縮性流れ

非圧縮性流れでは、速度場の発散 Θ がゼロなので、速度場の発散を含む項を落として

{\frac {D{\boldsymbol {v}}}{Dt}}={\frac {\partial {\boldsymbol {v}}}{\partial t}} ({\boldsymbol {v}}\cdot \nabla ){\boldsymbol {v}}=-{\frac {1}{\rho }}\operatorname {grad} p {\frac {\mu }{\rho }}\Delta {\boldsymbol {v}} {\frac {1}{\rho }}\operatorname {grad} ({\boldsymbol {v}}\cdot \operatorname {grad} \mu ) {\frac {1}{\rho }}\operatorname {rot} ({\boldsymbol {v}}\times \operatorname {grad} \mu )-{\frac {1}{\rho }}{\boldsymbol {v}}\,\Delta \mu  {\boldsymbol {g}}

となる。

粘性率が一定の流れ

粘性率 μ や χ は温度や圧力の関数であり一定ではないが、粘性率を定数と仮定する場合は、粘性率の勾配を含む項を落として、

{\frac {D{\boldsymbol {v}}}{Dt}}={\frac {\partial {\boldsymbol {v}}}{\partial t}} ({\boldsymbol {v}}\cdot \nabla ){\boldsymbol {v}}=-{\frac {1}{\rho }}\operatorname {grad} p {\frac {\mu }{\rho }}\Delta {\boldsymbol {v}} {\frac {\chi  {\frac {1}{3}}\,\mu }{\rho }}\operatorname {grad} \Theta  {\boldsymbol {g}}

となる。また、体積粘性率 χ は非常に小さいので、χ = 0 と仮定すると、

{\frac {D{\boldsymbol {v}}}{Dt}}={\frac {\partial {\boldsymbol {v}}}{\partial t}} ({\boldsymbol {v}}\cdot \nabla ){\boldsymbol {v}}=-{\frac {1}{\rho }}\operatorname {grad} p \nu \Delta {\boldsymbol {v}} {\frac {\nu }{3}}\operatorname {grad} \Theta  {\boldsymbol {g}}

となる（ストークスの仮説）。ここで ν = μ/ρ は動粘性率である。

粘性率が一定の非圧縮性流れ

粘性率が一定の非圧縮性流れでは、

{\frac {D{\boldsymbol {v}}}{Dt}}={\frac {\partial {\boldsymbol {v}}}{\partial t}} ({\boldsymbol {v}}\cdot \nabla ){\boldsymbol {v}}=-{\frac {1}{\rho }}\operatorname {grad} p \nu \Delta {\boldsymbol {v}} {\boldsymbol {g}}

となる。ここで ν = μ/ρ は動粘性率である。各項はそれぞれ、

左辺 - 第1項：時間[微分]項、第2項：移流項（対流項）
右辺 - 第1項：圧力項、第2項：粘性項（拡散項）、第3項：外力項

と呼ばれる。外力項は、状況によって、重力をはじめ浮力・表面張力・電磁気力などが該当する。

ストークス流れ（クリープ流れ）: 粘性率が一定の非圧縮性流れのうち、流体の速度が遅かったりスケールが小さいなど、レイノルズ数が小さい流れを特にストークス流れあるいはクリープ流れという。ストークス流れでは、非線型である対流項 $({\boldsymbol {v}}\cdot \nabla ){\boldsymbol {v}}$ が無視できて、; ${\frac {D{\boldsymbol {v}}}{Dt}}={\frac {\partial {\boldsymbol {v}}}{\partial t}}=-{\frac {1}{\rho }}\operatorname {grad} p \nu \Delta {\boldsymbol {v}} {\boldsymbol {g}}$; となる。この式はストークス方程式（Stokes equations）と呼ばれ、線形方程式のため基本解が知られている。例としてクエット流れやハーゲン・ポアズイユ流れがある。

オイラー方程式

粘性のない（χ = μ = 0）流れでは

{\frac {D{\boldsymbol {v}}}{Dt}}={\frac {\partial {\boldsymbol {v}}}{\partial t}} ({\boldsymbol {v}}\cdot \nabla ){\boldsymbol {v}}=-{\frac {1}{\rho }}\operatorname {grad} p {\boldsymbol {g}}

となる。この式はオイラー方程式と呼ばれている。

ポテンシャル流れ

渦度（速度場の回転）がない流れ

{\boldsymbol {\omega }}=\operatorname {rot} {\boldsymbol {v}}=\mathbf {0}

の場合には、ベクトル解析の定理により

{\boldsymbol {v}}=\operatorname {grad} \Phi

となる速度ポテンシャル Φ が存在する。

近似

ブシネスク近似: 熱輸送を伴う流れにおいて、温度による密度変化が大きくないとして扱う近似法をブシネスク近似という。

境界層近似: 流れが主流方向を持ち（逆流、再循環および剥離がない）、幾何的な変形が緩やかなときに行う近似法を境界層近似という。

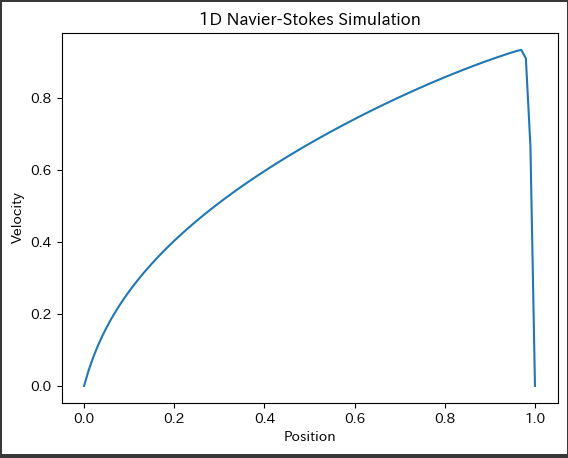
数値シミュレーション

もし一般解が求まれば、流体の挙動を完全に知る事ができることになるが、未だに一般解は発見されていない。また、解の存在可能性についても明らかとはなっておらず、物理学と数学の両方にまたがる重要な課題の一つとなっている（詳細は、ミレニアム懸賞問題、ナビエ–ストークス方程式の解の存在と滑らかさを参照）。従って、極めて特殊な制約条件の問題を除いて数値解析によって近似的に解を求める。

流体の数値シミュレーション（数値流体力学、CFD）では、このナビエ–ストークス方程式と連続の式、その他必要に応じてエネルギー保存の法則（熱対流）やマクスウェルの方程式（磁気流体力学）、状態方程式などを連立して、数値的に解くことで流体の挙動を予測する。

移流と拡散両方に関係している現象であるので、クーラン数、拡散数の両方を満たすようにシミュレーションを行う必要がある。

性質

乱流

乱流は流体の多くの流れで見られる時間依存のカオス的な振る舞いである。全体としての流体の慣性にそれがしたがうことが一般に信じられている。それゆえ慣性の効果が小さな流れは層流となる傾向がある。移流と粘性の強さの比率はレイノルズ数と呼ばれる無次元量であり、レイノルズ数がある閾値を越えると、微小なかく乱が移流項の非線型性により拡大していき、流れ場は非定常な乱流となる。

一方、右辺の粘性率を含む項（粘性項）は乱流の変動を抑制する効果を持つ。あまり深く理解されていないにもかかわらず、ナビエ‐ストークス方程式が乱流の性質を正確に記述することが信じられている。計算に対して計算時間が有意味に解き得るようになるちょうどよい計算メッシュによる解のようなこの要求条件の安定した解または直接数値シミュレーションの、乱流に関するナビエ‐ストークス方程式の数値解は、極度に困難である。難易度はその乱流に含まれている混合長さの尺度の違いに強く依存する。適当に変換するのに役立たない、層流を解くものを用いて乱流の流れを解く試みは、非定常解で典型的な結果を残す。

これに反して、レイノルズ平均ナビエ-ストークス方程式（RANS）のような、乱流モデルを補った時間平均方程式は、乱流をモデル化するときに実用的な数値流体力学（CFD）の応用で用いられる。追加の方程式を加えてRANSを導く、Spalart-Allmaras乱流モデル、k‐ω乱流モデル、k‐ε乱流モデルを含む幾つかのモデルは、Large eddyシミュレーション（LES）がこれらの方程式を数値的に解くように用いるようにもできる。RANSよりも計算時間と計算機メモリーの面で、これらのアプローチは電子計算機で行うには大変コストがかかる。しかし、それは陽的に大きな乱流の尺度を分解するのでより良い結果を生み出すのである。